スイングバイの実験(かなりいい加減です)
(2005/12/08作成)
人工衛星を加速させる方法に「スイングバイ」という方法があります。
まずは実行してみましょう。
使い方
・「Start」を押すとシミュレーションを開始します。
・「Stop」を押すと一時的に停止します(また「Start」を押せば再開します)。
・「Clear」を押すと、元の状態に戻ります。
・「地球の上からスイングバイ」を選択すると「上から下」もしくは「下から上」へのスイングバイするように設定を変えられます。
(衛星の初期位置を少しずらしています)
※注意 地球と衛星が近づくと時間間隔を小さくしているため、ゆっくり動いて見えます。
このシミュレータはかなり重いです。
誤差を小さくするため時間間隔をかなり小さくしてるためです。
それでも誤差はでかいようですが・・・。オイラー(Euler)法で計算してます。
Java Applet版はこちら。
解説など
スイングバイ、とは惑星の重力と公転運動を利用して衛星を加速させる技術のことです。
最近話題の探査機「はやぶさ」が「イトカワ」からサンプルを採取(したかも)して地球に
向けて帰還中ですが、
はやぶさも「イトカワ」に向かう途中で地球とスイングバイをして加速しています。
(基本的のこのページは「はやぶさ」に感化されて作りました)
で、上はかなりいい加減なスイングバイの実験です。
衛星が地球の公転速度(29.7Km/s)の65%の速度(秒速19.3Km)で太陽の周りを公転しています。
で、地球を利用して加速しよう、というシミュレーションです。
真ん中の白い円が太陽で(大きさは適当)で緑の線が地球。赤の線が人口衛星です。
衛星が地球に近づくと、ちょっと時間の刻みをゆっくりにして、さらに画面の下のほうに
拡大して表示します。
地球の半径が6400Kmぐらいですが衛星は6800Kmぐらい、とほとんど地球にぶつかるぐらい
まで近寄ってスイングバイします。
スイングバイした後は、明らかに軌道の形が変わって、そして軌道が少し大きく
なっているのが分かります。これは衛星が地球の公転エネルギーからエネルギーをもらって
加速したためです。
(逆に地球の公転速度はほんのちょっぴり落ちています。が無視できるほど小さいです)
太陽を中心にして考えると、衛星の位置エネルギーと運動エネルギーの合計は
位置エネルギー
U = -G*M*m / R (G:重力定数,M:太陽の質量,m:衛星の質量, R:太陽からの距離)
運動エネルギー
E = m*v*v / 2 (m:衛星の質量, v:衛星の速度)
U+E = -696000000 * m (スイングバイ前)
U+E = -616000000 * m (スイングバイ後)
と、+80000000 * m 増えています。
(画面の右にオレンジでグラフが出ます。これには地球からの位置エネルギーは含まれていません)
これを最初の地点で、どのくらい加速されたかに換算してみます。
速度 v から a*v とa倍に加速されたとすると、
m* (v)* (v)/ 2.0 - U = E1
m*(a*v)*(a*v)/ 2.0 - U = E2
U は同じなので消去して
m* (v)* (v)/ 2.0 - E1 = m*(a*v)*(a*v)/ 2.0 - E2
a で整理して
a*a = 1 + 2*(E2-E1) / (m*v*v)
E2 - E1 = +80000000 * m
で、最初の速度が地球の公転速度、29.7 Km/s の65%なので、v = 19.3 Km/s = 19300 m/s
これから
a*a = 1 + 2* (80000000 * m) / (m*19300*19300) = 1.4295 平方根をとって
a = 1.1956 倍 なので
a * v = 1.1956 * 19.3 = 23.1 Km/s
なので 19.3Km から +3.8 Km/s ほど(進行方向に)加速されていることになります。
逆に減速させることも出来ます。地球より少し速い速度(1.1倍 32.7Km/s)で公転している衛星が
地球の進行方向の前方を通ることで減速することが可能です。( シミュレーションでは -4.3 Km/s ほど減速されたことになります。)
なぜ加速されるのか?
これが最初はとても疑問でした。
衛星が惑星に近づいてくれば確かに加速されますが、遠ざかるにつれて速度は
遅くなって、結局、元の速度に戻ってしまうのではないか、と。
これは正しいです。
じゃあなぜ加速されるのかというとそれは「視点の違い」なのだと思います。
・惑星から見ると衛星は遠くからやってきて、また遠くに去ってしまう。速度は全然変わらない。
のですが
・太陽からみると、たまたま惑星がそこを通りがかるために、速度が変わったように見える。
ということです。
つまりどこを基準に速度を計るか、ということですね。
一番、衛星が加速されるケースは、下のように、惑星の正面からやってきて、正反対に
飛ばされるケースです。
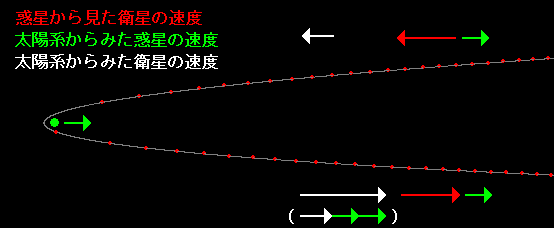
惑星から見た衛星の動き。(遠くから双曲線を描いてやってきて、また去っていくように見える)
結局、最大でも加速される速度は「惑星の公転速度の2倍」が限度ということになります。
(地球だと公転速度は30Km/sなので最大でも60Km/s、木星だと13Km/sなので最大でも26Km/sの加速が限度となります。)
(減速される場合は惑星の真後ろからやってきて、また真後ろに戻る場合で、最大は同様に公転速度の2倍です)
しかし、重力が小さい惑星だとあまり軌道に影響を与えませんし、
惑星から遠い場所だと重力も小さいので、こんなに軌道は曲がりません。
また惑星の半径が大きいと、あまり接近できないので軌道の変化も小さくなります。
結局、
1. 惑星の公転速度
2. 惑星の質量
3. 惑星の半径
この3つでどのくらい加速できるかが決まってくるのではないかと思います。
そして、惑星の進行方向と同じ方向に離脱するように、進入速度と角度を調整すれば、
最大の加速を得ることが出来るとのことです。
外部リンク
Wikiの
スイングバイの解説 英語での解説。
「はやぶさ」が行う予定のスイングバイ
(地球と同じ速度(30Km/s)から、地上3700Kmまで近づき、4Km/sほど加速)
「はやぶさ」が行ったスイングバイの結果 地球や月を撮影した写真など。
木星探査機ガリレオが行った
スイングバイ
(PDF,11ページ目)。いったん逆方向の金星に行き、金星、地球、地球とスイングバイしています。
土星探査機カッシーニが行った
スイングバイ。
いったん逆方向の金星に行き、金星、金星、地球、木星とスイングバイしています。
Javaのソースはこちら。
参考にしたページ
ルンゲクッタ法について(数値解析)
元のページに戻る

