ピタゴラス三体問題のシミュレーション
ピタゴラス三体問題のシミュレーション
(2005/12/15作成)
ピタゴラス三体問題とはピタゴラスの三角形(三辺の長さが3,4,5の直角三角形)が
あるとき、その頂点に、それぞれ重さ3、重さ4、重さ5の物体を置いたときに
万有引力だけでどんな運動をするか、というシミュレーションです。
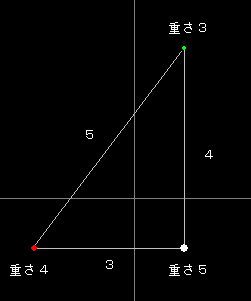
ピタゴラス三体問題の初期配置
1913年にブラウ(C.Burrau)によって研究され、1967年にエール大学のサブヘイ(Szebehely)らに
よって解決された問題とのことです。
(パソコンで見る天体の動き(長沢 工 著、地人書店出版、1992) より)
ここでは、それをルンゲクッタ法で解いてみます。
この3体問題はずばり「誤差との戦い」です。
途中で、物体同士が非常に接近し、万有引力の力も非常に大きくなるので、
その時、あまり時間間隔を大きくして計算してしまうと誤差も大きくなってしまい、使い物にならなくなります。
参考文献では補外法と、物体が接近したときに「正則化」という方法で別の微分方程式に
変換して解いてるのですが、難しかったので(汗)、ルンゲクッタ法で、接近したときだけ
計算間隔を小さくする方法で逃げています。
シミュレーションは40秒後くらいまではまぁ正確なのですが、50秒を過ぎると有効数字で3桁程度しか
精度がなくなってます。
この問題の正解は、最後は m3 は右上に弾き飛ばされて、m4 と m5 は互いに回転しながら
左下に去っていく、というのが正しい計算結果とのことです(参考文献より)。
一応、シミュレーションでも似たような最終図まではたどり着きます。
ちなみに、最初はオイラー法で解いてみたのですが、かなり間隔を小さくしても
誤差が大きくなりすぎて、最終図(ぽいもの)にはたどり着けませんでした。
使い方
・「Run」を押すとシミュレーションを再開します。
・「Stop」を押すと一時的に停止します(「Run」を押せば再開します)。
・「ピタゴラス数」で初期状態のピタゴラス数を設定できます。大きな値の時には座標全体を縮小させてます。
・「Set」を押すと、現在の設定されている3つの重さで開始します。直角三角形の形に自動的に配置されます。重心は原点とは限りません。
※注意 物体が近づくと時間がゆっくり進むので、実時間の動きをシミュレーションしたものではありません。
※補足 3つの物体の重心は常に動かないそうです。初期位置は重心が原点にくるように配置されています。
Java Applet版はこちら。JavaScriptより快適に動作します。
10ごとのtに対する三体の座標(パソコンで見る天体の動き、p183より)
この数値に合えば正しく計算してることになります。
t x3 y3 x4 y4 x5 y5
0.0 1.00000 3.00000 -2.00000 -1.00000 1.00000 -1.00000
10.0 0.77848 0.14139 -2.02509 0.09722 1.15299 -0.16261
20.0 3.00429 0.51193 -1.38863 -0.47048 -0.69167 0.06923
30.0 0.85634 2.28709 -0.87798 -0.86596 0.18858 -0.67949
40.0 -0.62200 1.85832 0.17354 -2.36841 0.23437 0.77974
50.0 -2.70146 -3.79722 1.50594 0.96081 0.41513 1.50968
60.0 0.74381 1.93995 0.26401 -0.73163 -0.65749 -0.57867
Javaのソースはこちら。
参考リンク
最終図はこちらで見れます。
project two -- Burrau's problem of three bodies
サブヘイが解いた論文(上のページのリンク中)。
(ポストスクリプトファイルですので読むのに Ghostview などのソフトがいります。)
Szebehely, V. 1967, "Burrau's Problem of Three Bodies",
Proceedings of the National Academy of Sciences of the United States of America, vol. 58, Issue 1, pp. 60-65
参考文献
パソコンで見る天体の動き(長沢 工 著、地人書店出版、1992 初版 第1刷)
元のページに戻る

